Galactic Colossi - The Formation And Mechanics Of Black Holes

Black holes are one of the most mind-boggling, cryptic secrets found in the universe; and, even with the many years of research gone into understanding them, we still have much left to uncover. Einstein predicted them, physical mathematicians corrobarated his claim, and recent telescopic images confirmed them - yet scientists still don't fully understand what black holes are. They are getting closer, however. Starting with a general overview of their anatomy, we are now aware that the size of black holes ranges from less than 1 solar mass (a unit that represents the mass of the Sun, just under 2 nonillion kilograms) to the trivial amount of 10 billion solar masses, with respective radii of 0.1 millimeter to over 60 billion kilometres in length. Accordingly, since the range is so great, we have set various terms to define individuals with different masses. These include: miniature black holes, stellar black holes, intermediate-mass black holes, supermassive black holes and ultramassive black holes.
Theoretically, no boundary really exists for these sizes. With sufficient energy, you could probably get a black hole that is larger than even our entire galaxy, the only limit being that astronomists have not found it yet. One thing that all black holes have in common, however, is their density. They are astonishingly dense, with so much mass packed into space that a black hole with the mass of the Earth would be as small as a typical marble...if that. This is also how black holes are created in the first place; a star or some other celestial figure becomes compressed so rapidly and powerfully that it eventually reaches a limit and morphs into its respective black hole. Consequently, we refer to this limit as the Schwarzschild radius, a concept derived by German astronomer Karl Schwarzschild in 1916 from an exact solution of Einstein's field equations. (Simplifying the complex mathematics of general relativity, this solution is based on the assumption that the charge and angular momentum of a spherical mass are zero, hence allowing you to consider only the mass of black holes to calculate their radius 'at rest'.) If you are curious, you can use a calculator and the equation below to work out the Schwarzschild radius of other items.
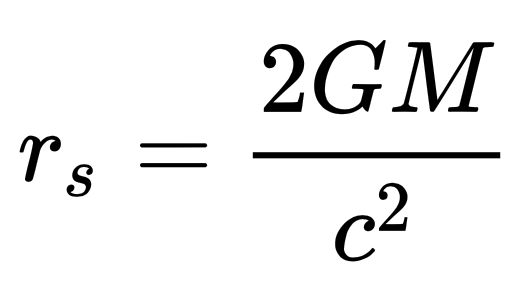
One manner by which a star might get compressed into a black hole is via a supernova explosion. Over time, nuclear fusion reactions in the core of a star counteract its gravitational force and cause it to grow. After eons of continuous expansion, however, the balance shifts; elements will have fused enough to produce iron (the most stable element in the universe), allowing gravity to start pulling the star's mass in. The ensuing implosion condenses all of the mass built up in the centre, increasing its density manifold and reflecting extraordinary shockwaves that spread throughout the galaxies - a supernova. Producing devastating waves of heat and radiation, these events are what first allowed researchers to identify the locations of black holes in our universe. We now understand, for example, that most galaxies revolve around a supermassive (or larger) black hole in the centre. Our own Milky Way is no exception - it features Sagittarius A*, a black hole that has around 4 million times the mass of the Sun.
Supernovae are also remarkably resourceful, decorating black holes so that they are rarely just lonely voids of death in the endless vacuum of space. But that raises a question - what do black holes actually look like?
The Structure Of Swirling Giants
Surrounding every black hole is a boundary known as the event horizon. Though this is not defined by any strict physical barrier that envelops its shape, it is what the public might know colloquially as the 'point of no return'. Speaking mathematically, the event horizon is where the escape velocity (the theoretical starting velocity required to completely leave the object's gravitational field) is exactly equal to the speed of light. Since nothing in the universe can travel faster than the speed of light, this means that anything with energy that goes past a black hole's event horizon - whether it is a human, a spaceship, or even light - will never be able to leave again. Scary, huh?

Fortunately, if you ever find yourself stuck in such a position and have miraculously not been dismantled by the black hole's immense forces, you will have quite a spectacle to accompany you. First, you might notice a great veil of colours and warped images flowing into your eyes. Light from celestial bodies all over the universe would get sucked in by the black hole, bending so that light from all angles enters the event horizon with you. The likely result: a wondrous panorama of all the stars and galaxies and nebulas from everywhere and anywhere possible. (A gift to the falling man.) This would also come with the electromagnetic radiation emitted by superheated debris orbiting the black hole away from its event horizon, the matter of which forms a Saturn-like ring of plasma and gas called the accretion disc.
Interestingly, light approaching the black hole does not necessarily have to move into it. It could also get affected by its gravity to bend and be deflected elsewhere, like a particularly quick vehicle moving into a roundabout. Otherwise, there is the rather unique situation where light simply remains stable in orbit around the black hole. Occurring only in a position widely known as the photon sphere, this section is located just outside the event horizon and might appear shadowy from the inside and outside of the black hole, with the light essentially being 'trapped' in circulation. This is due to the gravitational strength being large enough to keep the light nearby, but still sufficiently small that it is not immediately pulled in. As such, if you could stay stationary in one place in the photon sphere, you would likely be able to witness any light reflected from the back of your head orbiting towards you. In an ideal world, you would eventually see yourself in front of you, giving rise to the illusion of a sort of clone of your immediate past. (A bit dramatic, but you get the gist of it.)
Finally, there are the astrophysical jets, also known as relativistic jets. Shooting perpendicularly to the accretion disc and away from the two poles of the black hole, these are portentous pillars made of superheated ionised matter (i.e., plasma) that has been accelerated to near-speed-of-light velocities and then spewn out of the body's axis of rotation. In turn, the shape of the jets is dependent on the magnetism of the system. Although black holes themselves are not known to carry any electic or magnetic fields, the wide expanses of rotating ions in the accretion disc do. Similar to how the Earth's magnetic field is generated, this flow of ions creates perpendicular electromagnetic fields that surround the black hole, consequently constricting the stream of outpouring particles into narrow jets. Depending on their given energy, relativistic jets have been known to travel about 300,000 times the radius of their host black hole, dispersing energy in the form of gamma radiation that we detect on Earth.

Interestingly, the sum of a black hole, an accretion disc and their astrophysical jets are collectively thought to have the most efficient energy-conversion mechanism possible. Incredibly enough, if you take the efficiency as a ratio of the energy taken away by the jets to the energy of the accreted matter, it may even exceed 100 percent! And if this was actually found to be the case, it would go against both the laws of thermodynamics and the conservation of energy and make our native physicists very excited, to say the least. Alas, it was not to be. Scientists have since found that some of the energy in a jet also comes from the black hole's rotation, slowing down to power the stream. Nevertheless, as the rotating accretion disc also drives the rotation of the black hole (and as matter from the universe is always being pulled into its gravitational field), black holes are still the most marvelous automated energy machines we have seen. In the age of space travel, it would be pretty cool if we could harness their energy somehow.
Now, while much of the above is fairly intuitive, there are some bits that are definitely weighing researchers down in the present. Namely, we have mentioned how general relativity plays into this - but what about quantum mechanics?
Black Hole Mechanics
All physical systems in our universe, physical or otherwise, are thought to always follow the laws of thermodynamics. One of these laws - the second law of thermodynamics - states that the entropy of the universe always increases. In brief terms, entropy is essentially a measure of how spread out energy is, so that, when it increases, there is more 'randomness' in a system. As such, you can imagine how confused scientists must have been when Einstein first told us about the existence of black holes, which at first were believed to have no entropy but nonetheless absorbed matter with the stuff. In other words, they seemed to gradually decrease the total entropy of the universe, contradicting everything we knew about thermodynamics.
Eventually, Israeli-American physicist Jacob Bekenstein postulated that black holes do have entropy. In a fortuitous turn of events, he then collaborated with American physicist Stephen Hawking to prove in 1971 that the entropy of black holes was proportional to one quarter of their surface area, and that said surface area could never decrease. This then became known as the second law of black hole mechanics - which, alongside three other laws involving the constancy of gravitational strength in the event horizon and such, constitutes part of black hole mechanics. But this has been a conundrum in science for a while now; you would think that, if anything, entropy would instead be proportional to volume. To help it make sense, physicists have since proposed theories like the Holographic principle, which states that all the activity in the universe can be reduced to a lower dimensional space (a hologram) wherein actual results can be interpreted. Some computers simulations have corroborated this theory; but, overall, it stands unproven.

Three years later, in 1974, Hawking further showed that black holes also emit photons at their boundary - now referred to as Hawking radiation - paradoxically decreasing the size of the black hole while still allowing its surface area to remain increasing. Combining quantum field theory with black holes, Hawking radiation makes the beginning of the link between quantum mechanics and general relativity. This is significant - particularly since it should lead to the answer to one of the greatest problems in science: quantum gravity. See, general relativity is not complete, containing inconsistensies like infinite densities (i.e., singularities) that should break the theory down. There is much experimental evidence that supports it, however, and so we are left to wonder how we might resolve such issues. The key, it would seem, is in the minute particle interactions of the quantum world - and it is only a matter of time before we find it.
References
- Harvey, A. L. W., Georganopoulos, M. & Meyer, E.T. (2020). Powerful extragalactic jets dissipate their kinetic energy far from the central black hole. Nature Communications 11:5475. Retrieved from https://doi.org/10.1038/s41467-020-19296-6
- Nokhrina, E. E. (2017). The Correlation between the Total Magnetic Flux and the Total Jet Power. Frontiers in Astronomy and Space Sciences 22. Retrieved from https://doi.org/10.3389/fspas.2017.00063
- Miller, J.M (2021). Slow black hole accretion drives mass loss. Nature Astronomy 5:873–874. Retrieved from https://doi.org/10.1038/s41550-021-01419-8
- Wald, R.M. (2001). The Thermodynamics of Black Holes. Living Reviews in Relativity 4:6. Retrieved from https://doi.org/10.12942/lrr-2001-6
- Cowen, R. (2013). Simulations back up theory that Universe is a hologram. Nature. Retrieved from https://doi.org/10.1038/nature.2013.14328
