Review: The Theory Of Relativity And The Universe

Our planet spins at a velocity of over 1600 kilometres per hour at the equator. When we stand parallel to and in line with the equator, we also move at the same velocity - and we only go faster by walking there in the same direction! If you stand some distance away from here - say, in northern Iceland or Greenland - the situation changes. Since the earth's spin decreases in speed with higher relative latitudes (a phenomenon that occurs with spinning spheres known as the Coriolis effect), suddenly, you are moving at the much slower velocity of some 700 kilometres per hour (which is admittedly still pretty quick). Yet, ignoring changes in temperature and the surround sights and such, you feel quite comfortably the same whichever place you stand on. How is this possible?

The answer lies with the most famous posthumous researcher of our time - the German physicist Dr Albert Einstein. More specifically, it has to do with his theory of relativity, which is the first of a list of pivotal discoveries that led to him being recognised as one of the greatest pioneers in science of his time. It is also quite unintuative and unendingly complicated - so much so that you could do an entire degree on the subject and still not have realised all of it. As such, we will only explore the basics and scratch the complexity hidden below for this blog post; an entire thesis would not suffice, otherwise! But, in any case, so we begin.

The Special Theory

Interestingly, relativity has been around as a concept for a surprisingly long time, since before even Einstein took notice of it. Indeed, he actually got his original inspiration from the overarching ideas of Newtonian mechanics, which essentially encompass all the simplified physical laws for motion and forces in our universe. (Think v=d/t, or f=ma.) The principle that he was most interested in (and the one he believed most flawed) was the one of Galilean invariance. As the name suggests, this theory was first brought up by Galileo Galilei, who described it in the year 1632 in his book, 'Dialogue Concerning the Two Chief World Systems'.

At the time, Galileo was rather interested in how perspectives of motion differed when one was either stationary on land or standing on a moving ship. He observed that, when thrown upward, a ball would seem to move vertically up and then down (with no apparent horizontal motion) to the person who tossed it. Comparatively, if the individual on the ship threw the ball upward, the person on land would see it move in a concave parabola until it landed again. The explanation for this was simple; motion is relative to the frame of reference that we are taking, so that a person on a ship moving at a constant speed feels that they are actually stationary, and that it is the world around them that is moving horizontally (opposite to the direction of the ship's motion). To the person on land, the opposite would be true and it would be the person and ball that would possess a horizontal velocity. Since there is no acceleration in either scenario, such frames of reference are referred to as inertial frames.

Most things in the universe only possess a relative motion. If we look at a shooting star, for example, it would appear to be moving at an extraordinary speed; but if we looked at it from a spaceship that is travelling at exactly the same velocity, it would in turn appear to be completely stationary. Indeed, from their frame of reference, it would be the rest of the universe that is moving towards them.

Now, there is a single little exception to this rule of relative motion, and it is the fact that light in a vacuum always moves at approximately 300,000 kilometres per second regardless of the frame of reference that it is in. First proved in 1887 when American physicists Albert Mickelson and Edward Morley used an interferometer to check if there was any absolute frame of reference in the universe (spoiler alert: there was not), the Mickelson-Morley experiment inadvertedly proved that light in a vacuum would move at the same speed no matter what your own velocity was. Now known as one of Einstein's two postulates of special relativity (the other being how classical laws of physical are the same in all inertial frames), the invariance of the speed of light has become crucial to understanding essentially all aspects of our universe. Causality, for example - which is how different events can be distinguished from one another in time - breaks down completely when an object in an arbitrary frame of reference is able to move faster than the speed of light. In such a case, strange theoretical phenomena would take place; time would move backwards to outside observers, the object moving would display an apparently greater-than-infinite kinetic energy (which admittedly does not make sense), and so on.

I should note that the use of the speed of light as a constant is only really a convenience to physicists, and is not always practically correct. Indeed, while light particles (photons) do travel at the upper possible speed limit in a vacuum, their speed can still decrease under the right circumstances - say, if light rays were refracted through a glass block. Any particle moving at that speed would also have the same invariance in all inertial frames, and so light is not special in that regard. As such, it would be more correct to say that the highest possible speed in the universe is actually the speed of causality - just about 300 million metres per second - and that even the fastest particles are simply limited from going faster than it. For now, however, we will stick with calling that upper limit 'the speed of light' - just for the sake of convenience.

Given the knowledge that the speed of light is constant in all inertial frames, then, how do the classical laws of Newtonian mechanics and Galilean invariance apply to it? To put it simply: they don't. With those rules, light that is emitted from and in the same direction as a moving train should technically be able to move faster than light emitted outside from a stationary lamp (at least in the lamp's frame of reference), but that does not happen experimentally. Instead, both rays move at exactly the same speed. Einstein was aware of this discrepancy - and so he came up with the concepts of time dilation and length contraction.

The Interconnected Universe Of Spacetime

In order to accomodate the quirky nature of particles moving at the speed of light, Einstein proposed (in his very famous 1905 paper, 'On the Electrodynamics of Moving Bodies') that different inertial frames had to use proportionally different coordinate systems in space and time, depending on their velocities relative to each other. Two objects that are stationary to each other would therefore experience the same changes in time and space, while an object moving away from them would not. In practice,  this would mean that a rocket flying away from us, for example, would appear to contract in length from our inertial frame (i.e., it would look shorter than when it was still on Earth). If we were able to view a clock on the moving rocket, then we would further observe that time is moving slower in the rocket relative to us.

In reality, these shifts in change of time and length occur at all speeds; from the inertial frame of a boy in the garden, even a moving slug would experience stretches in time and space. Practically, though, the factor by which these conversions happen (known as the Lorentz factor) is only significant at very high velocities. This is why people accepted the laws of Newtonian mechanics for so long - they had neither very fast vehicles nor the equipment to accurately compare the dimensional changes between a standing man and a donkey leaping from the attic (or something of the sort).

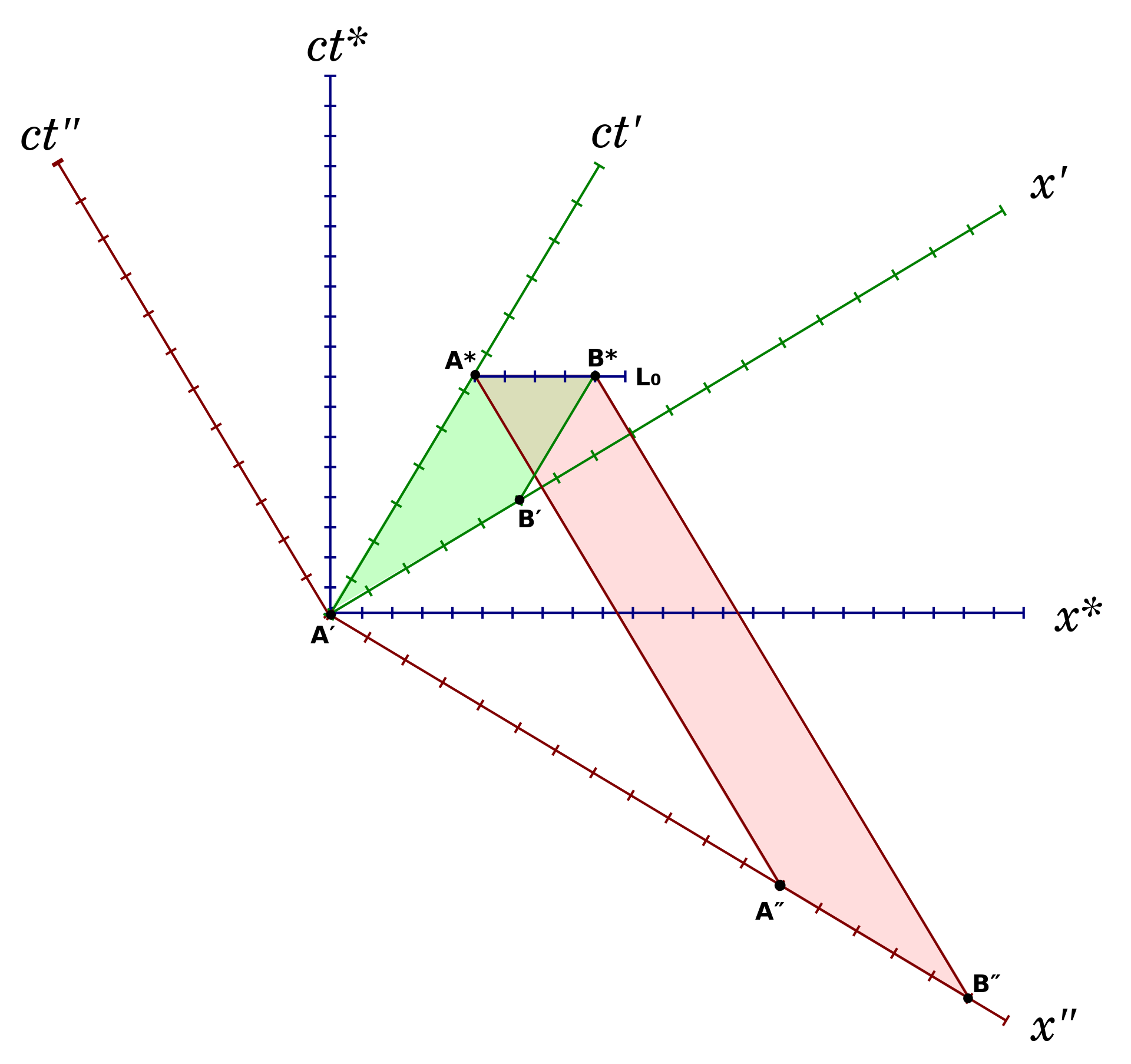
With this in mind - and again contrary to classical mechanics - we now find that space and time are not really separate entities at all. Each one relies on and changes depending on the other, and so the theory of special relativity gave rise to spacetime. When taking relativity into account, there are not three dimensions of space and one of time - but simply four dimensions of spacetime. This is demonstrated visually by a fantastic set of graphs known as Minkowski spacetime diagrams, named in 1908 after Einstein's ETH Zurich professor Hermann Minkowski. Although the mathematics behind these can get somewhat complicated (particularly when you include all four dimensions), they form a lovely representation for how the Lorentz transformation works. Since we are still dealing with non-accelerating objects, it is also important to understand that the different coordinate systems are all correlated linearly (again displayed by Minkowski diagrams). In other words, there is no bending of spacetime in special relativity, making the theory exclusive to...most situations in real life.

Acting as a simplistic model for relative motion, special relativity deals exclusively with inertial frames and does not consider the effect of changing velocities and universal forces like gravity. This is why so many scientists were at first doubtful of the theory, and why they were absolutely blown away when Einstein expanded it to include all motion only ten years after he'd begun.

The General Theory

Needless to say, general relativity is substantially more complex than special relativity. One key aspect of it is that, in the vicinity of objects with mass, spacetime curves around those objects in a non-linear manner to produce varying coordinate systems and the concept of gravity (as other objects with energy bend in the direction of the spacetime warp). To convert between these coordinate systems, you must then use multivariate mapping functions that consider changes in energy potentials (such as the metric tensor) before interpreting the results - all mathematically. Though such calculations are complex and definitely not properly demonstrable in one article, we can use their results to explain some astounding properties of our universe.

In the same vein, we can use mathematics to prove that energy and mass are interchangeable, with 1 kilogram of mass equalling approximately 90 quadrillion Joules of energy (which is quite a lot, I must say). Having realised this, Einstein was further able to demonstrate with his famous field equations - which relate the curvature of spacetime with factors like momentum, energy density and local pressure - that both accelerating and massive objects can bend spacetime. More generally, energy can bend and is affected by the bending of spacetime. Although it has no rest mass, light has momentum and hence an energy magnitude of its own, making it very much susceptible to the phenomenon. Alongside the existence of gravitational waves and black holes (which is a whole other topic of its own), this is how scientists first proved relativity; they observed light bending around celestial figures such as the sun in a solar eclipse.

Ultimately, however, researchers are still not aware of why energy warps our universe like this. Some speculate that it has to do with string theory, or perhaps some undiscovered quantum particles of interest. At the very least, we know that it happens. So, the next time someone asks you why the weekend seems to go so fast, you can assuredly tell them this: "That's just relativity at work."

References

• Einstein, A. (1916). Relativity: the special and the general theory. Crown Publishers.
• Choquet-Bruhat, Y. (2015). Introduction to General Relativity, Black Holes and Cosmology. Oxford University Press.