The Chaotic Transition States In Chemical Reactions

Usually, the smaller the object, the more jittery and excited it is. Parents will be well aware of how hyperactive little children can be, for example, with puppy-owning families exemplifying just how well they can imitate and get along with their dog. Smaller creatures like mice are even more pronounced in this aspect. Working with a model organism of the sort requires that you take the utmost precaution that they don't run off - which becomes all the more challenging when you're dealing with things like flying insects. (It is a wonder how fruit flies can move so fast in a confined space. But I guess we've all had our fair amount of frustration with the bugs before, haven't we?) While animals can seem to be remarkably speedy for their size, however, no creature comes close to the breakneck velocities that simple molecules can take.

Using a few mathematical equations in thermodynamics and classical mechanics, it is fairly trivial to work out that (at room temperature and pressure) even the heaviest molecules in the air regularly travel at over 500 metres per second. This is even higher than the speed of sound - and it is meagre when compared to the chaotic motion associated with subatomic particles. Depending on the number of atoms and molecules in the surroundings, an electron in an atom can orbit its nucleus at a magnitude of several thousand kilometres per second! They can go so fast, in fact, that physicists must take the theory of relativity into account when assigning them quantitative values.

For now, we will be backtracking a bit to look in more detail at the kinetics of molecules in space. In particular, given the industrial importance of accurately predicting the mechanisms behind chemical reactions, I'll be focusing on our understanding of what is referred to as a reaction coordinate. This is admittedly a rather general term, but it is essentially the parameter that tells us how far a reaction has proceeded. Time would be an example of a reaction coordinate; and entropy, a measure of how spread out and chaotic energy is, would, too (as we'll see at the end). By studying this, we not only gain comprehension of the turbulent nature of a reaction - but also of matter's primordial tendency towards chaos.

Transition State Theory

Let's say we pour into two separate conical flasks two different solutions, the first containing p-aminophenol with hydrochloric acid (as the latter chemical is used to fully dissolve the former) and the other featuring acetic anhydride. The first flask, we place in a preheated water bath, gently allowing it to warm for some time. After it reaches the water's temperature, we then mix in a sodium acetate buffer to neutralise the pH (i.e., removing the excess hydrogen ions from the solution) and immediately add the acetic anhydride into the flask. Making sure to mix well with a stirring rod to quicken the reaction, we take the flask out of the hot water bath and transfer it into an ice-cool bath - consequently causing our desired product to crystallise into a crude version of itself.

By processing the crystals through the means of filtration and recrystallisation, we get the purified product of the reaction between p-aminophenol and acetic anhydride: acetaminophen. Popular for its application in relieving headaches, joint aches and fevers, this drug is commonly used as a substitute to aspirin, particularly by the people who have unwanted side-effects to it. As it is, acetaminophen is better recognised under the trade name Tylenol - and so we begin to see how important these reactions can be for the pharmaceutical industry.

Crucial to the process - and to any chemical reaction, for that matter - are the movements of the dissolved particles in solution. Such is the case because, asides from a sufficient energy on collision, molecules must possess the correct orientation relative to each other in order to react. This is widely referred to as collision theory. In combination with the fact that electromagnetism is generally the only force involved in chemical reactions, these ideas have come to form and precede one of the greatest overarching concepts in all of chemistry: reaction mechanisms.

When studying any form of interaction between molecules, scientists often depict the pathway by which it occurs via the motion of electrons and pairs of electrons. Both are represented by curly arrows (an actual scientific term), though lone-electron arrows have one barb while the pairs have two. In addition to the molecules' structural formulas (i.e., etched models for how their constituent atoms and molecular bonds are arranged in space), this typically results in a sequence of structures and arrows showing the individual steps in the reaction. This part is vital, and so I repeat - chemical reactions occur in steps. Accordingly, a reaction mechanism is a representation of all the steps in a reaction. Some reactions, like the production of acrylic paint, occur in a few principal steps that are repeated to form polymers. Other times, the reaction becomes so extensive that it branches off into many hundreds of mechanisms and thus thousands of unique steps - notably taking place when cooking food.

In the case of Tylenol synthesis, there are only three steps to be concerned about. Being a wonderful example of a nucleophilic attack, p-aminophenol first uses its nitrogen's lone pair of electrons to attack a carbon atom in acetic anhydride. As this causes the carbon-oxygen double bond (wherein four electrons are shared between the atoms) to break, the produced intermediate then rearranges its electron pairs to re-create the double bond, in turn kicking out an acetate group from the molecule. Lastly, the acetate takes away a hydrogen ion from the second intermediate to end up with the uncharged products of the reaction.

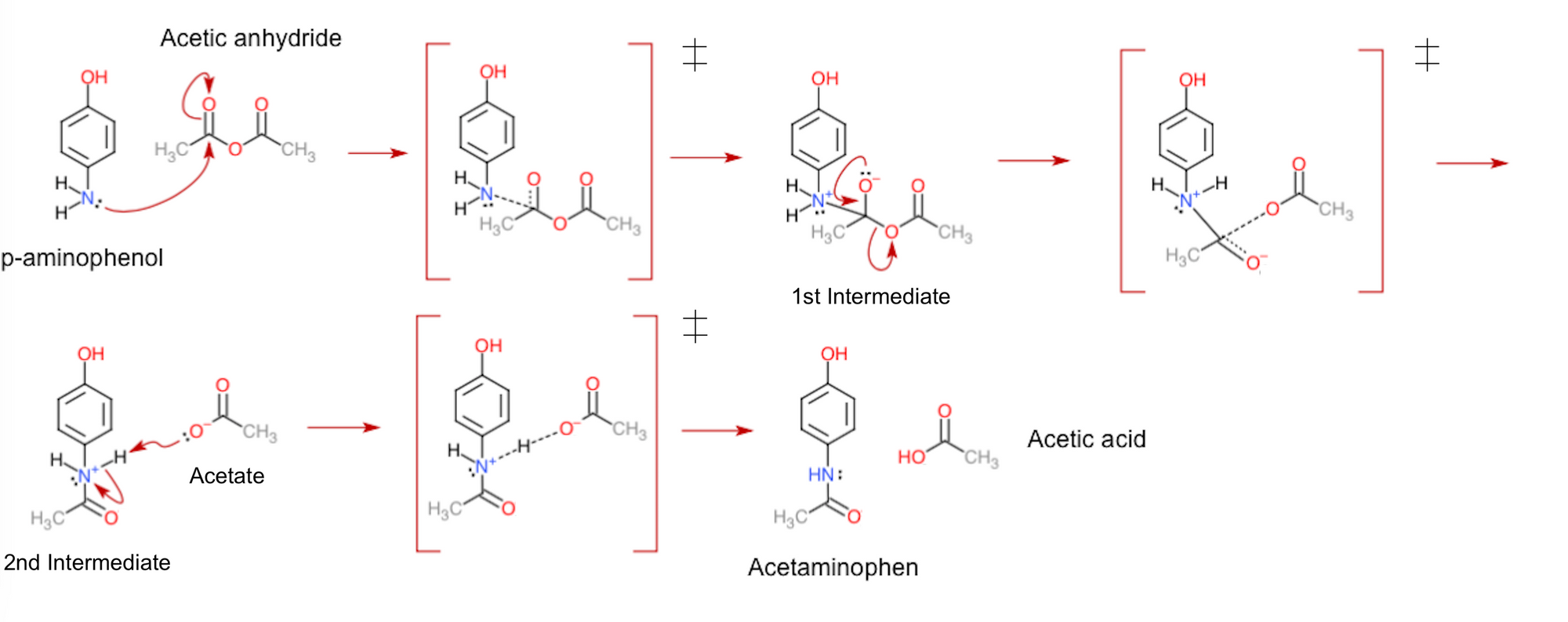
From the displayed mechanism above, you may notice that there are actually a few more stages to it than I mentioned. To be exact, after each reactant or intermediate produced, there appears to be a structure with a box and double dagger symbol (‡) surrounding it. Known as transition states, these figures are the in-betweens of each step in the reaction. They are the way the molecules would look during the time that they're exchanging electrons. The dashed lines portray this; these depict the bonds forming and breaking while electrons are transferred, consequently making them more transient than the other bonds in the molecules.

Importantly, transition states are not classified as intermediates. This is due to how intermediates can be separated and stored for practical periods of time in the lab (i.e., they are metastable). Comparatively, transition states have only ever been seen to exist for (at most!) microseconds at a time, and only in the artificial conditions used for research. In other words, these structures are unstable, and so can only ever exist as molecules are changing. Interestingly, the direct observation of the structure of transition states is currently one of the major challenges in modern chemistry, making it all the more necessary to understand how they function. To this end, transition states can be represented in potential energy diagrams like the one below. These show the change of energy inside molecules while they are converted from reactants to products.

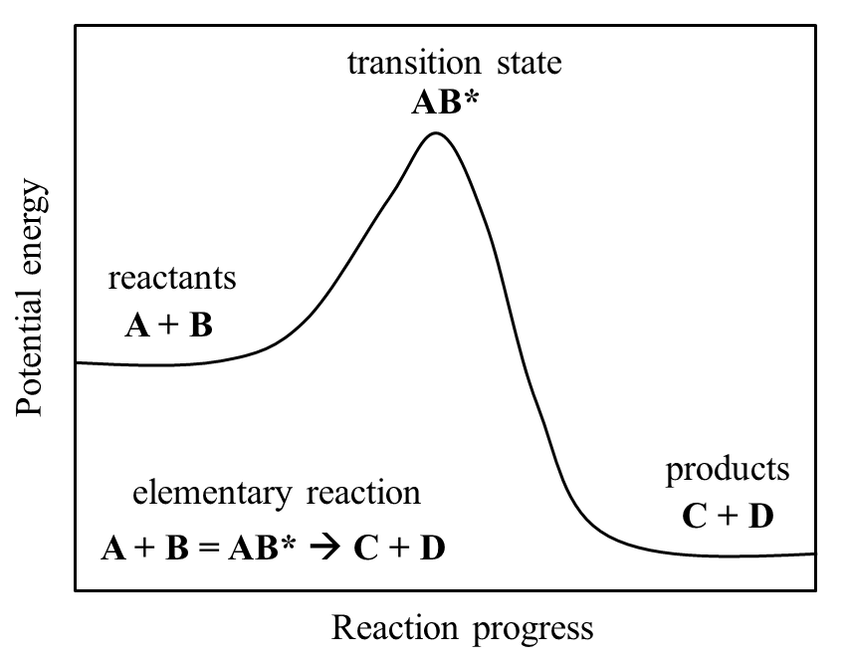
As matter is more stable in lower energy states, we can see from the diagram that a transition state is, in fact, less stable than its neighbouring forms. We could think of it as a football balancing on the peak of a hill. After reaching that point, the ball would fall to one side of the hill almost immediately, most often moving where the hill is at its steepest (in this case in the direction of the products). In Tylenol synthesis, we would need two more 'hills' on the diagram to describe all the steps in the middle of the reaction. Unfortunately, however, there is a catch to doing all this. Just as how molecules' behaviour is generally chaotic and uninterpretable, chemical reactions don't just occur in one way only. These models we give them, where molecules A and B combine into a specific transition state to then form products, are too simple. As such, much work has been does to overcome this issue, both computationally and theoretically. Fortunately, it also seems to be paying off.

Quantum Paths

Since transition state theory was first established in the 1920s to 1930s, equations in quantum mechanics have given us much insight into how they occur. Allowing us to consider phenomena like electron tunnelling and superposition, we are now able to lay the foundations for transition states as short-lived resonance states.

I should note here that scientists really like to apply semantics to practically everything and more, but it is vital to not get hung-up on them too much. While they can help specify certain procedures in nature, for our purpose, the important thing is to understand the concept. In this case, resonance states refer to chemical structures that happen at the same time as each other, only converging into one when the object is detected (say, by a ray of light hitting it). Unlike the original transition states, these are continuous and are subject to particle-wave equations, with different resonance states having higher probabilities of being detected as single molecules in space. The distinction is small, but it is important - for this means that we can work with transition states using quantum statistical models.

One application for transition state theory is to calculate the rate for a given reaction. By taking the barrier between reactants and products to be the transition state, we can model it to be a kind of multi-dimensional 'potential energy surface' with sloped distances to reactants and products that are proportional to the number of reactions that pass through the transition state. Then, through the quantisation of the translational, rotational and vibrational degrees of freedom of the molecules, we can add further parameter to the energy surface to optimise its shape and position. This minimises errors and identifies the most likely pathways of a reaction, letting us more accurately predict its overall rate. First developed in 1984, this method of optimisation has been dubbed variational transition state theory (VTST). It is also suitable for machine learning and accelerated discovery, making it incredibly useful in chemistry research.

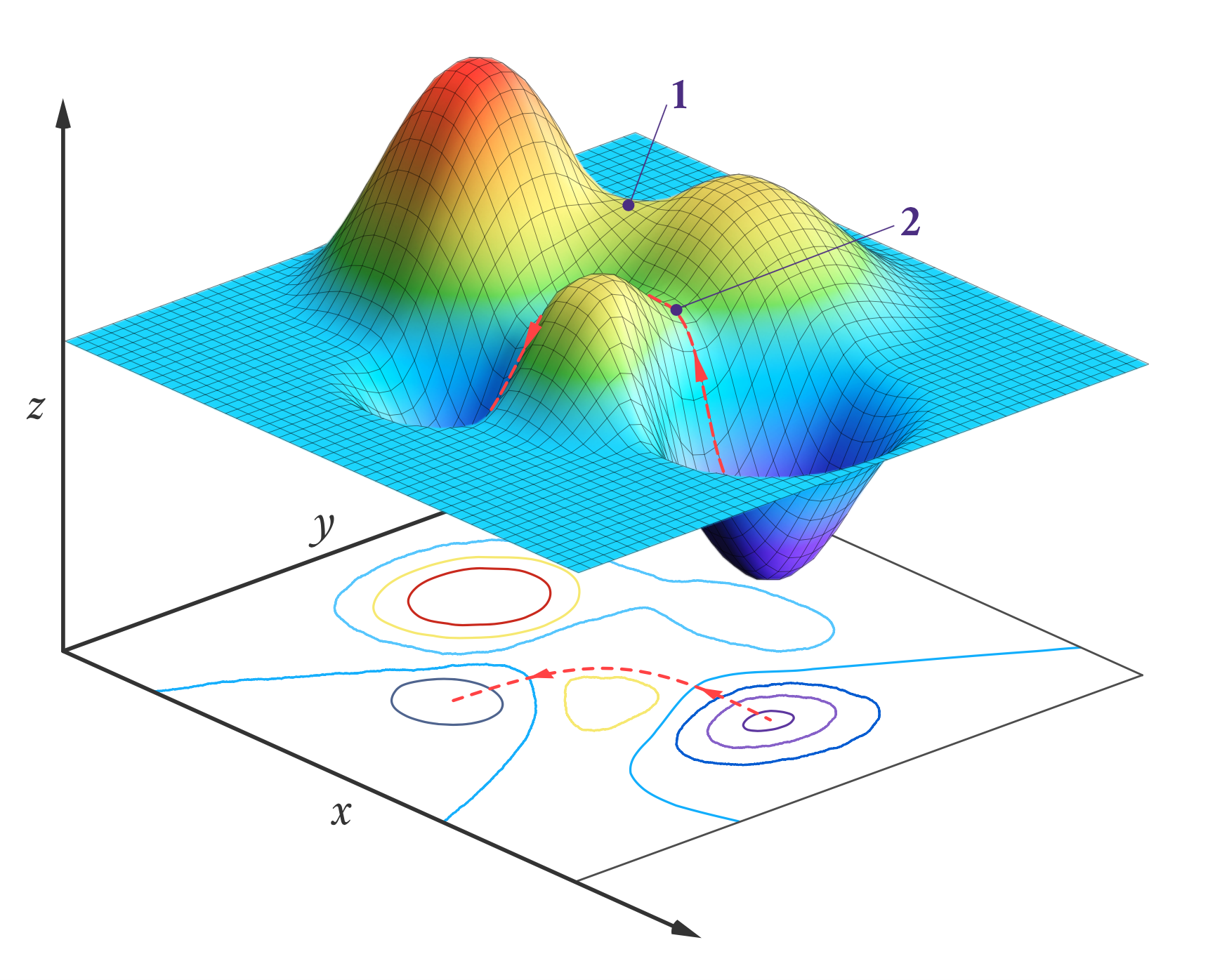
While VTST can be wonderful for theoretical analysis, however, it does not give us much information about the mechanisms themselves. How does A and B turn into C and D? Which bonds are broken and formed in the process? Analytical chemists solve this issue by using transition path sampling. Here, a computer program simulates the transition steps of a reaction a large number of times to see which steps turn reactants into products, over time assigning probabilities of occurring to each transition path. Not only does this result in a more representative picture of the reaction - including any rare events that would otherwise stay unnoticed experimentally - it also tells us of a variable that measures how probable it is for a given path to happen.

The committor, as it is called, has recently been explained by Miranda Louwerse and David Sivak of Simon Fraser University, Canada. The researchers proposed that it can actually be interpreted as the amount of entropy produced by a given reaction path, so that that the more entropy is produced, the more chance it has of happening. This makes sense, as all paths in a reaction share identical net potential energy changes (since reactants and products are the same), tying the amount of entropy generated directly to the feasibility and rate of a reaction path. Scientists have long-since known entropy to be crucial in chemical reactions - particularly in biological events like protein folding and enzymatic reactions. Nevertheless, the confirmation is good to have. Now we know for certain: reactions are not just chaotic, they prefer to be that way, too.

References

• Bao, J. L. & Truhlar, D. G. (2017). Variational transition state theory: theoretical framework and recent developments. Chemical Society Reviews 46:7548-7596. Retrieved from https://doi.org/10.1039/C7CS00602K
• E., W., Vanden-Eijnden, E. (2006). Towards a Theory of Transition Paths. Journal of Statistical Physics 123:503. Retrieved from https://doi.org/10.1007/s10955-005-9003-9
• Louwerse, M. D. & Sivak, D. A. (2022). Information Thermodynamics of the Transition-Path Ensemble. Physics Review Letters 128:170602. Retrieved from https://doi.org/10.1103/PhysRevLett.128.170602